Proliferation Saturation Index to Characterize Response to RT and Evaluate Altered Fractionation in Head and Neck Cancer

Abstract

Objective: To personalize radiation therapy dose fractionation protocols, it will be necessary to first quantitatively describe tumor volume reduction dynamics and subsequently simulate the results of alternative fractionation schemes.

Methods and Materials: The proliferation saturation index (PSI) model of tumor volume dynamics was fit to weekly tumor volume data from computed tomography scans of n = 39 head and neck cancer patients who received 66 to 70 Gy in standard daily fractions or with accelerated fractionation. Using the outputs of this model, we additionally simulated how these patients would respond to hyperfractionation with 1.2 Gy fractions twice a day. We identified PSI values that would improve responses and outcomes to hyperfractionation compared to single daily fractions.

Results: The PSI model fit volumetric tumor response dynamics data with high accuracy (R² = 0.92) using patient-specific PSI values. Simulations of an alternative fractionation protocol demonstrated that a subset of patients with intermediate PSI values could potentially have improved locoregional control by switching to hyperfractionation.

Conclusions: This is the first demonstration of the PSI model fitting data from head and neck cancer patients, and the results suggest a benefit from alternative fractionation schemes for a selected subset of patients.

Head and neck cancers (HNC) are commonly treated with definitive radiation therapy (RT) with or without systemic therapy, with RT being the single most common oncologic treatment.^1,2 Few inroads have been made to synergize biological and quantitative approaches with radiation biology and radiation oncology methodologies to personalize and optimize RT. Standard treatment is 56 to 70 Gy in 1.8 to 2 Gy fractions once daily with or without concurrent chemotherapy,¹ derived from maximum tolerable dose concepts and dose-escalation trials premised on a “one-size-fits-all” RT dose. Current radiation oncology clinical practice is that every patient receives the same treatment, planned strictly on pre-radiation American Joint Committee on Cancer (AJCC) TNM stage (Tumor size, lymph Node involvement, Metastasis presence), without regard to individual tumor dynamics that may influence RT outcome. Oropharyngeal cancer still represents significant heterogeneity within the same stage group. Thus, it remains unclear why some patients with similar clinical stage, treated with identical RT dose and dose fractionation, are cured while others are not. There is a strong need for personalized RT for individual patients.³

Adaptive RT delivery has been suggested primarily for anatomical and spatial adjustments during the course of treatment.⁴ Although alternative fractionation schemes have been tested in clinical trials with modest improvements from altered fractionation, it is possible that these benefits may be offset by increased toxicities across the cohort.⁵ This sets up the need to be able to identify specific patients who may benefit from alternative fractionation protocols. To rigorously evaluate every possible radiation dose and dose fractionation is experimentally and clinically unfeasible.⁶ However, the burgeoning field of integrated mathematical oncology may make such analyses possible. The integration of quantitative approaches could provide novel, reliable biomarkers based on mathematics and patient-specific disease dynamics to guide RT treatment personalization.^7-9

Mathematical modeling in radiation oncology has a long history, with the linear-quadratic (LQ) model,^10-14 biologically effective dose (BED),^15-19 tumor control probability,^20–22 and normal tissue complication probability (NTCP)^23-25 being widespread in research and practice. Recent mathematical modeling and simulation studies of the canonical radiobiological principles have led to the concept of temporally feathered radiation therapy (TFRT). In TFRT, different treatment plans are developed for each weekday of fractionated radiation to spare organs at risk in fractionated radiation schedules.^26,27 In close collaboration with experimental biologists, a mathematical model of glioma response to radiation has been calibrated and validated to develop and subsequently experimentally confirm radiation protocols that optimally counteract stem cell de-differentiation dynamics.²⁸

One mainstay of mathematical modeling in radiation oncology is to simulate the volume regression profiles during RT,^29-33 and to predict responses to a variety of dose and dose fractionation protocols.^33-37 Previous analyses revealed that parameters of complex models may be impossible to determine with limited clinical data,³⁸ suggesting that the number of patient-specific parameters must be kept to a minimum to avoid overfitting and model uncertainty. To this extent, the novel concept of a proliferation saturation index (PSI) has been previously introduced to simulate non-small cell lung cancer patient-specific response to RT with a single parameter.^39,40 Mathematical analysis revealed that PSI can robustly describe clinical data for a wide range tumor growth models.⁴¹ Here we show that the PSI model can simulate head and neck cancer patient-specific responses to RT with data from two clinical cohorts from Moffitt Cancer Center and MD Anderson Cancer Center. We then use the model to run in silico comparisons of a hyperfractionation protocol to identify which patients may most benefit from hyperfractionated radiation.

Methods and Materials

Patient Data

A total of 39 head and neck cancer patients were treated with 66 to 70 Gy RT with and without concurrent chemotherapy. Seventeen patients were treated at Moffitt Cancer Center where they received a total of 66 to 70 Gy RT in 2 Gy weekday fractions with concurrent chemotherapy, and the remaining 22 patients were treated at MD Anderson Cancer Center where they received a total of 66 to 70 Gy RT (2 or 2.12 Gy weekday fractions or with accelerated fractionation) with half of the patients receiving concurrent chemotherapy. The patient cohort was comprised of different primary sites (oropharyngeal, laryngeal, nasopharyngeal), HPV status, and clinical stage (stage T1-T4). Patient characteristics for the two cohorts are detailed in Table 1.

Tumor volumes were delineated on weekly cone-beam computed tomography (CBCT) or CT-on-Rails system combining a GE Smart Gantry CT scanner (GE Healthcare) and a 2100EX linear accelerator (Varian) (256 total CT-scan-derived tumor volumes). It should be noted that contouring tumor volumes from CBCT scans is highly dependent on adequate image quality. Insufficient contrast, obstruction of the tumor by other patient anatomy, and other factors may prevent delineation of tumor volumes. We only included tumor volumes from patients who had contourable images. Nearly 50% of the patients considered for the study had inadequate image quality and were thus excluded. Locoregional control censored up to 5 years was abstracted as outcome measure and determined by biopsy confirmation or imaging sufficient to initiate additional treatments.

Mathematical Model

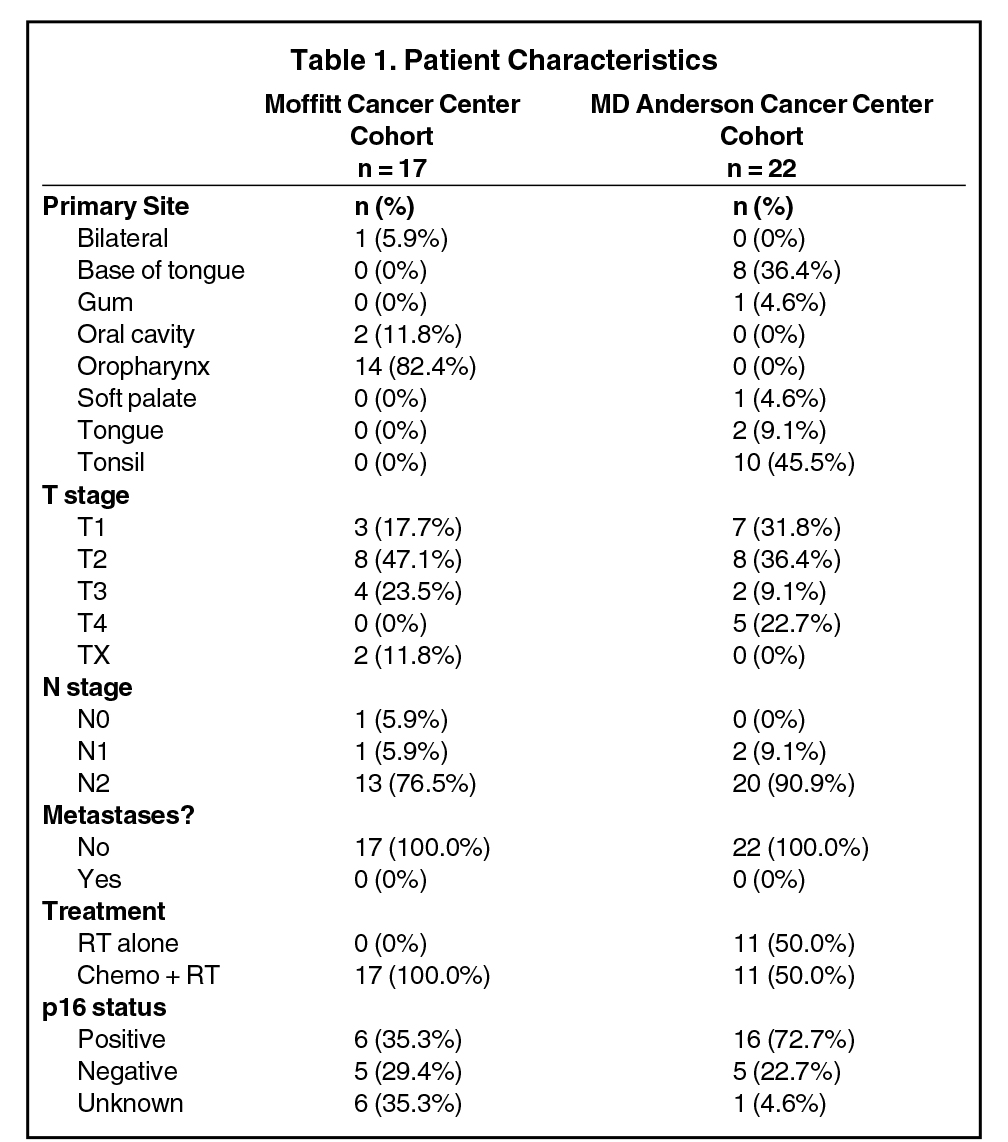
Tumor growth was modeled as logistic growth as governed by the following differential equation:

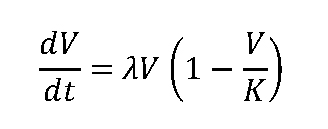
where λ is the intrinsic volumetric growth rate [day^-1], V is the gross tumor volume [cc], and K is the tumor carrying capacity [cc], which is defined as the maximum tumor volume that the local tissue can support. We have previously proposed characterizing individual patient tumor growth rates with the PSI, as opposed to the patient-specific growth rates.⁴¹ PSI is defined as the ratio of the initial tumor volume at the start of RT, V₀, to the tumor carrying capacity:

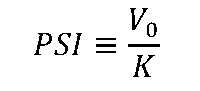
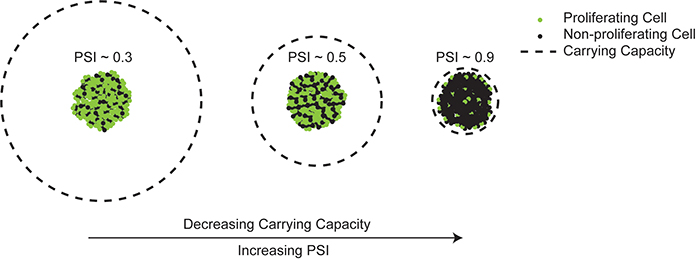
PSI is defined between 0 and 1 and PSI represents the fraction of nonproliferative cells in the tumor (Figure 1).

Response to radiation was modeled using the linear-quadratic (LQ) model:¹³

where SF(d) is the surviving fraction of cells after receiving a radiation dose, d [Gy]; and α [Gy^-1] and β [Gy^-2] are radiosensitivity coefficients. This is connected to the change in tumor volume by assuming that only proliferating cells are killed by radiation, in line with the Norton-Simon hypothesis that the rate of tumor regression under therapy is proportional to the tumor growth rate.^42-44 The change in tumor volume with each radiation fraction is modeled as follows:

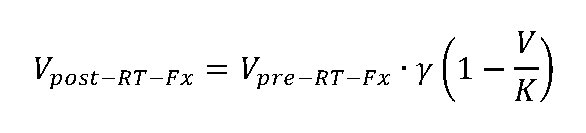
where γ is the volumetric death term per radiation fraction that is coupled to the LQ model as follows:

Implementation and Optimization

Custom scripts were written in MATLAB (Mathworks) to simulate volume trajectories given inputs of fractionation schedule, dose per fraction, λ, PSI, α, and α/β. To evaluate the ability of the model to fit the patient data, an optimization script was written using the particle swarm optimization function from the MATLAB Global Optimization Toolbox to find patient-specific PSI values, given a particular (λ,α) pair for the entire cohort, assuming α/β = 10 Gy. The optimal values for λ and α were found by performing a full grid search over λ ∈ (0.02, 0.18) day^-1 with a step size of 0.025 and α ∈ (0.04, 0.25) Gy^-1 with a step size of 0.01 to find the (λ,α) pair that minimized the mean square error to the patient data across the entire cohort for the first 4 weekly measurements.

Results

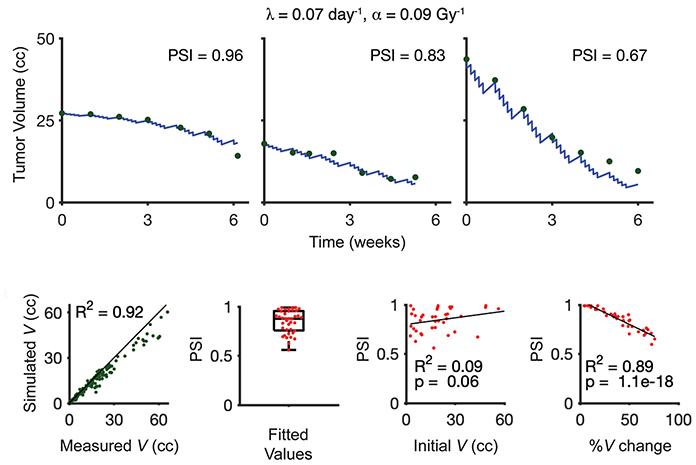
The parameter optimization identified that the values of λ = 0.07 day^-1 and α = 0.09 Gy^-1 best fit the tumor volume dynamics across the entire patient cohort. Although the values of λ and α were the same for all patients, the patient-specific PSI values allowed the model to fit both shallow-volume regression dynamics (high PSI) and rapid-volume reduction responses (low PSI) with high accuracy (Figure 2A). Across the entire cohort, the model fit the weekly tumor volumes with high confidence; R² = 0.92 (Figure 2B). Notably, while PSI was allowed to range from 0 to 1, only values > 0.5 were obtained from the fitting procedure using the optimized λ and α values, which indicates that the model was not overconstrained or overfitting the data (Figure 2C).

To assess the clinical significance of the model parameters, we compared patient-specific clinical measures with the fitted model parameters. Initial tumor size did not correlate with PSI (Figure 2D), but percent change in tumor volume after 4 weeks of RT showed a strong correlation with PSI (Figure 2E).

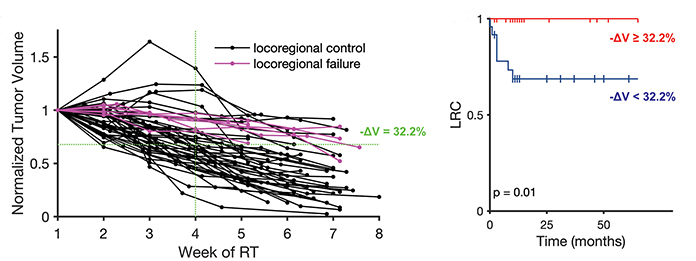
To translate tumor volume reduction to long-term patient outcomes, we tested midtreatment tumor volume reduction as a predictor for locoregional control (LRC). We found that the median tumor volume reduction at week 4 (-ΔV = 32.2%) perfectly separates out those patients who had early locoregional recurrence (Figure 3). This is comparable to the recent observation that midtreatment nodal decrease ≥ 43% in oropharyngeal cancer is prognostic for locoregional control.⁴⁵

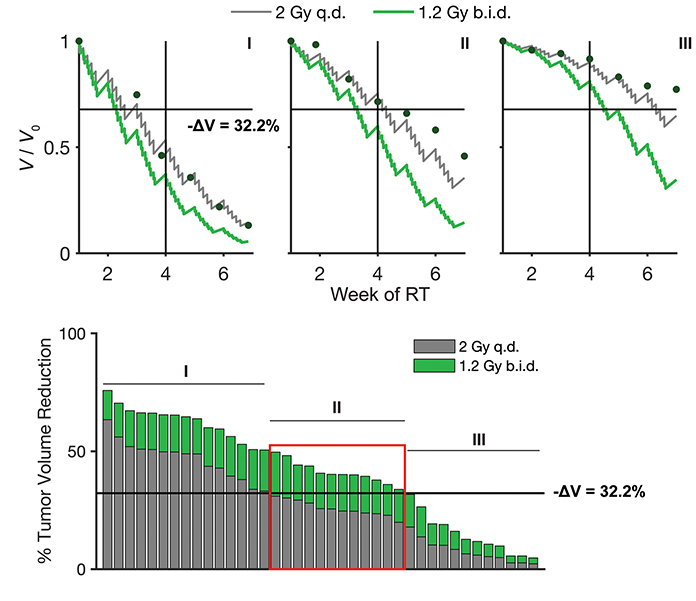
Given that the standard protocol with 2 Gy weekday fractions results in a subset of patients recurring locoregionally, we simulated an alternative hyperfractionation scheme of 1.2 Gy fractions 2 times a day (1.2 Gy BID). These simulations were performed using the previously optimized λ, α values across the cohort, and patient-specific PSI values. As expected, these simulations predicted that all the patients would have increased tumor volume reduction due to the higher total dose (Figure 4A). However, only a subset of patients with intermediate PSI ([0.835-0.91], Case II: 12/38 patients, 32%) is predicted to have sufficient marginal increase in tumor volume reduction to cross the previously determined volume-reduction threshold for LRC, indicating a potential to benefit from a switch to hyperfractionation (Figure 4B). On the other hand, patients with low PSI values have highly proliferative and radiation-sensitive disease (PSI < 0.835; Case I: 15/38, 39%), with both 2 Gy QD and 1.2 Gy BID yielding midtreatment tumor volume reductions > 32.2% indicating no additional benefit from hyperfractionation. On the other extreme, patients with high PSI values have less proliferative and more radioresistant tumors (PSI > 0.91; Case III: 12/38, 32%), and in this case neither fractionation protocol provides robust midtreatment tumor volume reduction.

Discussion

Herein, we presented a simple mathematical model based on proliferation saturation index, PSI, that was able to characterize head and neck cancer patient-specific volume changes to fractionated RT with only 1 patient-specific parameter with high accuracy. Notably, the growth rate is assumed to be constant across the entire cohort, and all interpatient heterogeneity is captured in the PSI values. Of interest, initial tumor size, and thusly T stage, did not correlate with PSI and midtreatment response. The need to only determine one patient-specific parameter may facilitate future patient-specific modeling and predictions. It may be possible to estimate patient-specific PSI values using midtreatment volume reduction, which was shown to correlate with PSI. Furthermore, these modeling results demonstrate that treatment response dynamics may provide valuable insights to understanding the nature of the disease. These results complement previous analysis of pretreatment tumor volume dynamics associated with outcomes in patients with oropharyngeal cancer.⁴⁶

Additionally, since the tumor volumetric death term was coupled to the LQ model, we were able to simulate the potential response to an alternative fractionation scheme of hyperfractionation with 1.2 Gy BID. Although hyperfractionation is not widely used in clinical practice to treat squamous cell head and neck cancers, large meta-analyses have shown an 8% difference in overall survival at 5 years post-treatment compared with standard fractionation.^5,47 However, this benefit may be offset by long-term toxicities from the increased overall dose and logistical difficulties in delivering multiple fractions a day. Mathematical models of tumor volume dynamics may eventually serve as part of a framework to identify patients who would benefit from hyperfractionation over standard fractionation.

It is important to note that the α values identified in this study are for radiosensitivity for the entire tumor volume and are not directly comparable to radiosensitivity parameters derived from clonogenic assays in vitro. With the correlation of locoregional control with a volumetric reduction threshold at 4 weeks of RT, we used these simulations to identify which patients could benefit from hyperfractionation to achieve robust midtreatment tumor volume reductions that correlate with locoregional control. This study demonstrates mathematical-modeling-derived PSI as a radioresponse biomarker in head and neck cancer and supports previous findings in non-small cell lung cancer that patients with intermediate PSI values may benefit from hyperfractionation protocols.

Of interest mathematically, it is difficult to accurately identify a unique (λ,α) parameter pair that fits the entire cohort, as other parameter pairs with the same λ/α ratio would yield similar model fits. Thus, it is important to accurately identify either the volumetric growth rate before the start of therapy or tumor radiosensitivity. This can potentially be accomplished with just two pre-treatment CT scans spaced a few weeks apart, such as at diagnosis and at treatment planning or simulation, similar to a previous study of tumor volumetric growth velocity.⁴⁶ Radiation sensitivity index, RSI, may be a candidate for radiosensitivity that will be explored in future studies.³ The alternative fractionation simulations are also limited by the canonical radiobiological assumptions of the LQ model. It will be important to verify whether this method of accounting for different dose sizes holds up in similar data with different doses per fraction.

Notably, our model cannot capture transient increases in tumor volume during the first few weeks of RT. These types of small increases in tumor volume, or pseudo-progression, in early weeks of treatment have been seen in the other studies. In a recent study of 44 node-positive oropharyngeal cancers,⁴⁵ the authors saw changes in nodal volume ranging from a 74.3% volume increase to a 73.6% volume decrease at day 10 of chemoradiation; a 48% volume increase to a 94.9.% volume decrease at day 20; and a -18.1% volume increase to a 95.6% volume decrease at day 35. This can potentially be addressed by building a model with a delayed effect of RT.

Conclusion

We acknowledge that this analysis was performed on a small number of patients (n = 39), but we would like to note that our methodology of analyzing longitudinal tumor volumes (6 to 8 CT scans per patient) increases total data points to n = 256 CT scans, significantly strengthening the analysis. The usability of this model in making patient-specific predictions and clinical recommendations still requires independent parameter calibration and validation in independent datasets with larger and more homogenous cohorts.⁴⁸ However, the results presented here are important steps in the mathematical modeling of RT response in this cancer type and demonstrate the potential for testing alternative treatment schemes in silico to inform the design of clinical trials for personalizing RT prescriptions.

References

1. Marur S, Forastiere AA. Head and neck cancer: changing epidemiology, diagnosis, and treatment. Mayo Clin Proc. 2008;83:489-501.
2. Marur S, Forastiere AA. Head and neck squamous cell carcinoma: update on epidemiology, diagnosis, and treatment. Mayo Clin Proc. 2016;91:386-396.
3. Mellon E, Yue B, Strom TS, et al. A genome-based model for adjusting radiotherapy dose (GARD): a retrospective, cohort-based study. Lancet Oncol. 2016;18(2):202-211. doi:10.1016/s1470-2045(16)30648-9
4. Veiga C, McClelland J, Moinuddin S, et al. Toward adaptive radiotherapy for head and neck patients: feasibility study on using CT-to-CBCT deformable registration for “dose of the day” calculations. Med Phys. 2014;41(3)031703.
5. Bourhis J, Overgaard J, Audry H, et al. Hyperfractionated or accelerated radiotherapy in head and neck cancer: a meta-analysis. Lancet. 2006;368(9538):843-854.
6. Enderling H, Kim S, Pilon-Thomas S. The accelerating quest for optimal radiation and immunotherapy combinations for local and systemic tumor control. Ther Radiol Oncol. 2018;2:1-3.
7. Enderling H, Alfonso JCL, Moros E, Caudell JJ, Harrison LB. Integrating mathematical modeling into the roadmap for personalized adaptive radiation therapy. Trends Cancer. 2019;5(8):467-474. doi:10.1016/j.trecan.2019.06.006
8. Aherne NJ, Dhawan A, Scott JG, Enderling H. Mathematical oncology and its application in non melanoma skin cancer--a primer for radiation oncology professionals. Oral Oncol. 2020;103:104473.
9. Anderson ARA, Quaranta V. Integrative mathematical oncology. Nat Rev Cancer. 2008;8(1):10-19. doi:10.14389/adr.4.10
10. Fowler JF. Fractionated radiation therapy after Strandqvist. Acta Radiol Oncol. 1984;23(4):209-216.
11. Dale RG. The application of the linear-quadratic dose-effect equation to fractionated and protracted radiotherapy. Br J Radiol. 1985;58(690):515-528.
12. Muller-Runkel R, Vijayakumar S. Equivalent total doses for different fractionation schemes, based on the linear quadratic model. Radiology. 1991;179(2):573-577.
13. Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 1989;62(740):679-694. doi:10.1259/0007-1285-62-740-679
14. Sachs RK, Hlatky LR, Hahnfeldt P. Simple ODE models of tumor growth and anti-angiogenic or radiation treatment. Math Comput Model. 2001;33(12-13):1297-1305. doi:10.1016/S0895-7177(00)00316-2
15. Diffey BL. A mathematical model of the biologically effective dose of solar UVA received by patients undergoing oral psoralen photochemotherapy for psoriasis. Phys Med Biol. 1981;26(6):1129.
16. Fowler JF. 21 Years of biologically effective dose. Br J Radiol. 2010;83(991):554-568. doi:10.1259/bjr/31372149
17. Orton CG. A unified approach to dose-effect relationships in radiotherapy. II: Inhomogeneous dose distributions. Int J Radiat Oncol Biol Phys. 1988;14(3):557-560.
18. Dale RG, Jones B. The effect of tumour shrinkage on biologically effective dose, and possible implications for fractionated high dose rate brachytherapy. Radiother Oncol. 1994;33(2):125-132.
19. Dahlman EL, Watanabe Y. Evaluating the biologically effective dose (BED) concept using a dynamic tumor simulation model. Med Phys. 2020.
20. O’Rourke SFC, McAneney H, Hillen T. Linear quadratic and tumour control probability modelling in external beam radiotherapy. J Math Biol. 2009;58(4-5):799.
21. Dhawan A, Kohandel M, Hill R, Sivaloganathan S. Tumour control probability in cancer stem cells hypothesis. PLoS One. 2014;9(5):e96093.
22. Chvetsov AV, Stewart RD, Kim M, Meyer J, Rengan R. Volume effects in the TCP for hypoxic and oxygenated tumors. Med Phys. 2020;47(9)4626-4633.
23. Colombo F, Francescon P, Cora S, Testolin A, Chierego G. Evaluation of linear accelerator radiosurgical techniques using biophysical parameters (NTCP and TCP). Int J Radiat Oncol Biol Phys. 1995;31(3):617-628.
24. Stocks T, Hillen T, Gong J, Burger M. A stochastic model for the normal tissue complication probability (NTCP) and applications. Math Med Biol. 2017;34(4):469-492. doi:10.1093/imammb/dqw013
25. Palma G, Monti S, Conson M, Pacelli R, Cella L. Normal tissue complication probability (NTCP) models for modern radiation therapy. Seminars in Oncology. 2019(46):210-218.
26. López Alfonso JC, Parsai S, Joshi N, et al. Temporally feathered intensity-modulated radiation therapy: A planning technique to reduce normal tissue toxicity. Med Phys. 2018;45(7):3466-3474.
27. Parsai S, Qiu RLJ, Qi P, et al. A step-by-step guide to temporally feathered radiation therapy planning for head and neck cancer. J Appl Clin Med Phys. 2020;21(7)209-215.
28. Leder K, Pitter K, LaPlant Q, et al. Mathematical modeling of PDGF-driven glioblastoma reveals optimized radiation dosing schedules. Cell. 2014;156(3):603-616.
29. Rockne R, Rockhill JK, Mrugala M, et al. Predicting the efficacy of radiotherapy in individual glioblastoma patients in vivo: a mathematical modeling approach. Phys Med Biol. 2010;55(12):3271-3285. doi:10.1088/0031-9155/55/12/001
30. Watanabe Y, Dahlman EL, Leder KZ, Hui SK. A mathematical model of tumor growth and its response to single irradiation. Theor Biol Med Model. 2016;13(1):1-20. doi:10.1186/s12976-016-0032-7
31. Wang P, Feng Y. A mathematical model of tumor volume changes during radiotherapy. Sci World J. 2013;2013.
32. Chvetsov A V. Tumor response parameters for head and neck cancer derived from tumor-volume variation during radiation therapy. Med Phys. 2013;40(3):34101.
33. Kyroudis CA, Dionysiou DD, Kolokotroni EA, Stamatakos GS. Studying the regression profiles of cervical tumours during radiotherapy treatment using a patient-specific multiscale model. Sci Rep. 2019;9(1):1-16. doi:10.1038/s41598-018-37155-9
34. Jeong J, Shoghi KI, Deasy JO. Modelling the interplay between hypoxia and proliferation in radiotherapy tumour response. Phys Med Biol. 2013;58(14):4897.
35. Jeong J, Oh JH, Sonke J-J, et al. Modeling the cellular response of lung cancer to radiation therapy for a broad range of fractionation schedules. Clin Cancer Res. 2017;23(18):5469-5479.
36. Arnesen MR, Hellebust TP, Malinen E. Impact of dose escalation and adaptive radiotherapy for cervical cancers on tumour shrinkage—a modelling study. Phys Med Biol. 2017;62(6):N107.
37. Kawahara D, Wu L, Watanabe Y. Optimization of irradiation interval for fractionated stereotactic radiosurgery by a cellular automata model with reoxygenation effects. Phys Med Biol. 2020;65(8):85008.
38. Chvetsov AV, Sandison GA, Schwartz JL, Rengan R. Ill-posed problem and regularization in reconstruction of radiobiological parameters from serial tumor imaging data. Phys Med Biol. 2015;60(21):8491.
39. Prokopiou S, Moros EG, Poleszczuk J, et al. A proliferation saturation index to predict radiation response and personalize radiotherapy fractionation. Radiat Oncol. 2015;10(1):1-8. doi:10.1186/s13014-015-0465-x
40. Sunassee ED, Tan D, Ji N, et al. Proliferation saturation index in an adaptive Bayesian approach to predict patient-specific radiotherapy responses. Int J Radiat Biol. 2019;95(10):1421-1426.
41. Poleszczuk J, Walker R, Moros EG, Latifi K, Caudell JJ, Enderling H. Predicting patient-specific radiotherapy protocols based on mathematical model choice for proliferation saturation index. Bull Math Biol. 2018;80(5):1195-1206. doi:10.1007/s11538-017-0279-0
42. Norton L, Simon R, others. Tumor size, sensitivity to therapy, and design of treatment schedules. Cancer Treat Rep. 1977;61(7):1307-1317.
43. Norton L, Simon R. Growth curve of an experimental solid tumor following radiotherapy. J Natl Cancer Inst. 1977;58(6):1735-1741.
44. Simon R, Norton L. The Norton--Simon hypothesis: designing more effective and less toxic chemotherapeutic regimens. Nat Clin Pract Oncol. 2006;3(8):406-407.
45. Byun DJ, Tam MM, Jacobson AS, et al. Prognostic potential of mid-treatment nodal response in oropharyngeal squamous cell carcinoma. Head Neck. 2020;43(1):173-181.
46. Perni S, Mohamed ASR, Scott J, et al. CT-based volumetric tumor growth velocity: a novel imaging prognostic indicator in oropharyngeal cancer patients receiving radiotherapy. Oral Oncol. 2016;63:16-22. doi:10.1016/j.oraloncology.2016.10.022
47. Lacas B, Bourhis J, Overgaard J, et al. Role of radiotherapy fractionation in head and neck cancers (MARCH): an updated meta-analysis. Lancet Oncol. 2017;18(9):1221-1237.
48. Brady R, Enderling H. Mathematical Models of Cancer: When to predict novel therapies, and when not to. Bull Math Biol. 2019;81(10):3722-3731.